Pour faire un kappa de Cohen ou de Fleiss, pas besoin d’une licence d’Office, R, logiciel libre et gratuit compatible Windows, macOS, Linux fait très bien l’affaire.
Si vous ne savez pas comment installer R, vous pouvez suivre le début de mon tuto sur R commander.
Bien formater ses données
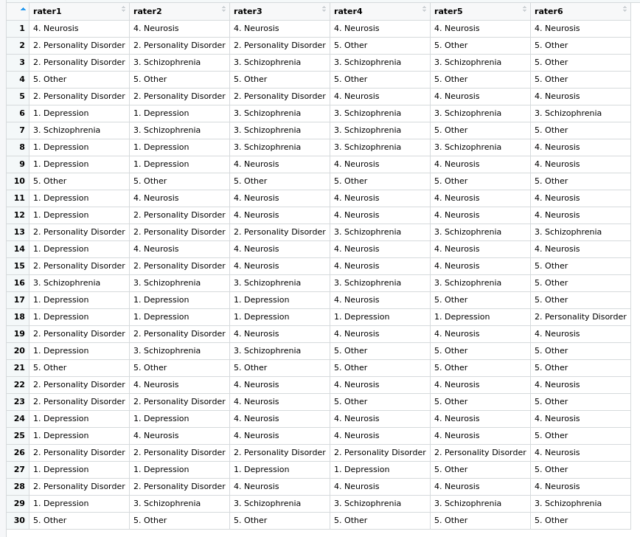
Pour illustrer la bonne manière de formater ses données, je vais prendre pour exemple le fichier diagnoses du paquet irr, qui simule le diagnostic de troubles psychiatriques de 30 patients par 6 médecins.
Il faudra donc organiser votre tableau en un praticien par colonne et un patient par ligne. Le kappa de Cohen concernera la mesure de concordance entre 2 praticiens, le kappa de Fleiss la mesure de concordance de plus de 2 praticiens.
Importer ses données
Si vous avez un fichier csv :
diagnoses > read.csv2(data.csv)
Faire un kappa de Cohen
Tapez les commandes suivantes en adaptant à votre cas :
install.packages("vcd") # si vcd n'est pas installé
library("vcd")
res.k <- Kappa(diagnoses)
res.k
La valeur value est le kappa.

Faire le kappa de Fleiss
Tapez les commandes suivantes en adaptant à votre cas :
install.packages("irr") # si irr n'est pas installé
library("irr")
kappam.fleiss(diagnoses)
Il est également possible de calculer un kappa de Fleiss par catégorie :
kappam.fleiss(diagnoses, detail = TRUE)

Interprétation du kappa de Cohen et de Fleiss
L’interprétation des kappa de Cohen et Fleiss est assez subjective. Les statisticiens que j’ai pu observer se basent généralement sur une table de Landis et Koch (1977) qui était prévue initialement pour interpréter un kappa de Cohen à deux classes :
| Valeur kappa | Niveau de concordance |
| < 0 | Pauvre concordance |
| 0.01 – 0.20 | Faible concordance |
| 0.21 – 0.40 | Légère concordance |
| 0.41 – 0.60 | Concordance moyenne |
| 0.61 – 0.80 | Concordance importante |
| 0.81 – 1.00 | Concordance presque parfaite |
N’oubliez pas également de prendre en compte dans le résultat la p-value calculée à partir du Z score. Cela vous indiquera jusqu’à quel point votre résultat est différent d’un score qui aurait pu être obtenu par hasard.

